The total circulation of the magnetic field around a small loop is given by \begin{eqnarray*} {\rm circulation} = \sum_{\rm box} \BB \cdot d\rr = (\grad\times\BB) \cdot d\AA \end{eqnarray*} where $d\AA=\nn\,dA$, where $\nn$ is perpendicular to the (filled in) loop.
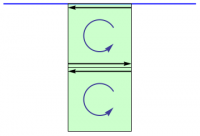
But any surface can be filled with such loops, as shown in Figure 1a. Furthermore, the circulation around the edge of the surface is just the sum of the circulations around each of the smaller loops, since the circulation through any common side will be zero (because adjacent loops have opposite notions of “around”), as indicated schematically in Figure 1b. Thus, the total circulation around any loop is given by \begin{eqnarray*} \oint\limits_{\rm loop} \BB \cdot d\rr = \Int_{\rm inside} \!\! (\grad\times\BB) \cdot d\AA \end{eqnarray*} This is Stokes' Theorem.
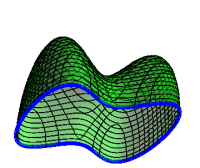
There is no need for the “inside” of the loop to be planar. 1) Consider the surface shown in Figure 1c, which has the same boundary as the original loop. The circulation around interior loops cancels just as before, and Stokes' Theorem holds without modification. We like to describe such surfaces as “butterfly nets”, whose rim is the original loop. Butterfly nets should be able to catch butterflies! In other words, they need an opening, and a net. 2)
The orientations used in the two integrals in Stokes' Theorem must be compatible. This is easy if the loop lies in the $xy$-plane: Choose the circulation counterclockwise and the flux upward. More generally, for any loop which is more-or-less planar, the circulation should be counterclockwise when looking at the loop from “above”, that is, from the direction in which the flux is being taken. (So you're really looking in the direction of negative flux.) An easy way to remember this is to take the flux up and the circulation counterclockwise when seen from above, with obvious modifications should the loop be sideways.
But what if the loop is not planar? What about a cylinder which is closed at one end? There are several strategies which can be used to obtain compatible orientations.
- Gears: Break up the surface into small loops, which can be thought of as small gears. Choose an orientation of the surface, and look at the surface from “above”. As the gears turn counterclockwise, the edge of the surface also turns; use that orienation to compute the circulation.
- Toothpicks: Think of the surface as a rubber sheet. Move the rubber sheet so that it is taut across the loop. Choose a compatible orientation using the “up” and “counterclockwise” rule. Now imagine putting toothpicks in the surface on the “up” side only, and move the rubber sheet back to the original position. The direction of the toothpicks gives you the compatible orientation of the surface.
- Left-Hand Rule: Walk around the edge of the surface, with your head up. That is, face in the direction $\TT$, with your head in the direction $\nn$ (where $d\rr=\TT\,ds$ and $d\SS=\nn\,\dS$). In a compatible orientation, your left hand should point along the surface; if it doesn't, turn around (or stand on your head, but not both).